

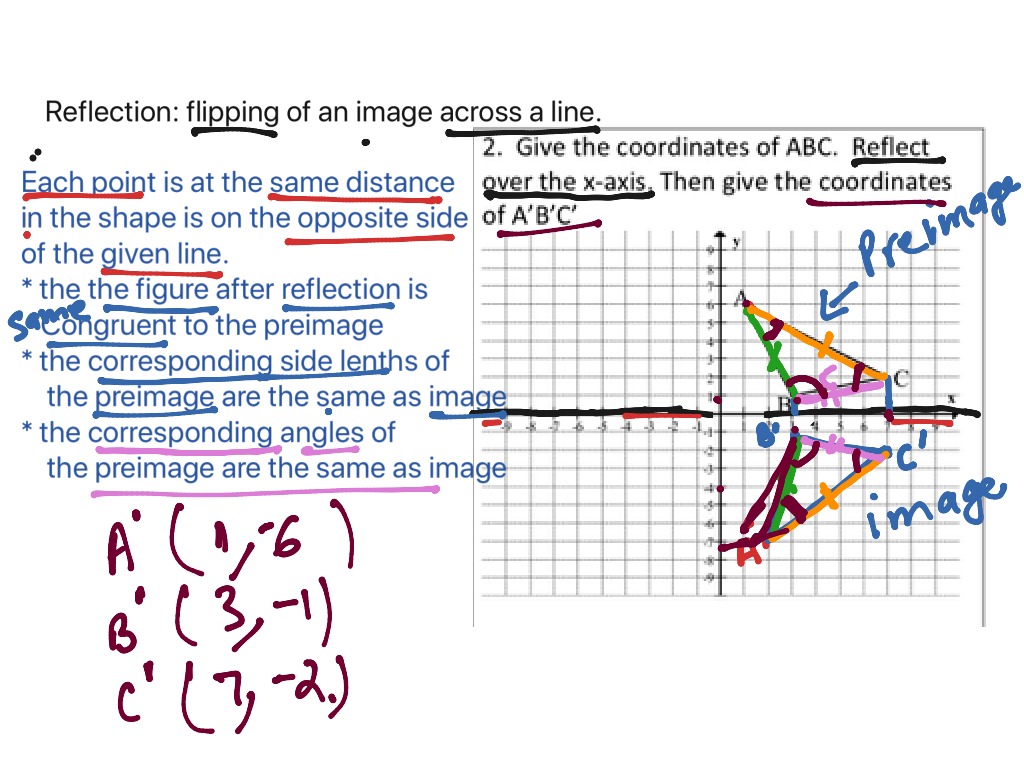
We know that a point (x, y) maps onto (-x, y) when reflected in the y-axis. There are different types of transformations and their graphs, one of which is a math reflection across the y-axis. Another transformation that can be applied to a function is a reflection over the x- or y-axis. Solved example to find the reflection of a point in the y-axis:įind the points onto which the points (11, -8), (-6, -2) and (0, 4) are mapped when reflected in the y-axis. (iv) The image of the point (-6, 5) in the y-axis is the point (-(-6), 5) i.e., (6, 5). (iii) The image of the point (0, 7) in the y-axis is the point (0, 7). An object and its reflection have the same shape and size, but the figures face in opposite directions. If the pre-image is labeled as ABC, then the image is labeled using a prime symbol, such as A'B'C'. The original object is called the pre-image, and the reflection is called the image. (ii) The image of the point (-3, -4) in the y-axis is the point (-(-3), -4) i.e., (3, -4). A reflection can be done across the y-axis by folding or flipping an object over the y axis. (i) The image of the point (3, 4) in the y-axis is the point (-3, 4). Therefore, when a point is reflected in the y-axis, the sign of its abscissa changes.
Similarly the coordinates of $B$ are $(-4,-4)$ while $C = (4,-2)$ and $D = (2,1)$.īelow is a picture of the reflection of each of the four points over the $x$-axis: Find the coordinates of the vertices of each figure after the given transformation. Answer (1 of 2): Remember that for a coordinate (x, y), the first entry represents the position on the x-axis, and the second entry represents the position on the y-axis. The coordinates of $A$ are $(-5,3)$ since $A$ is five units to the left of intersection of the axes and  3 units up. In order to help identify patterns in how the coordinates of the points change, the teacher may suggest for students to make a table of the points and their images after reflecting first over the $x$-axis and then over the $y$-axis: Point Thus the knowledge gained in this task will help students when they study transformations in the 8th grade and high school.Â


Later students will learn that this combination of reflections represents a 180 degree rotation about the origin. Reflection over the y axis: When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is transformed into its opposite. This means that if we reflect over the $x$-axis and then the $y$-axis then both coordinates will change signs. Similarly when we reflect a point $(p,q)$ over the $y$-axis the $y$-coordinate stays the same but the $x$-coordinate changes signs so the image is $(-p,q)$.Â.When we reflect a point $(p,q)$ over the $x$-axis, the $x$-coordinate remains the same and the $y$- coordinate changes signs so the image is $(p,-q)$.The reflection of the point (x, y) across the. The teacher may wish to prompt students to identify patterns in parts (b) and (c): Reflections in the Coordinate Plane: Reflecting over the x-axis: (the x-axis as the line of reflection). For each of my examples above, the reflections in either the x- or y-axis produced a graph that was. We really should mention even and odd functions before leaving this topic. That means that the y-values would stay the. The goal of this task is to give students practice plotting points and their reflections. Reflection in y-axis (green): f(x) x 3 3x 2 x 2. The y-axis is the vertical axis, so if we were to reflect a function over the y-axis, we would do a horizontal flip.


 0 kommentar(er)
0 kommentar(er)
